Section 7.3 Filtered Complexes
We will now describe how every filtered complex gives rise to a spectral sequence. We will be writing a homological spectral sequence, but by setting slightly different conventions one could also write a cohomological spectral sequence; this part is up to your personal taste. Given a filtered complex \((C, \partial, F)\text{,}\) we first, define
\begin{equation*}
E_{p, q}^{0}:=F^{p} C_{p+q} / F^{p-1} C_{p+q}
\end{equation*}
and let \(d_{0}: E_{p, q}^{0} \longrightarrow E_{p, q-1}^{0}\) be the differential induced on the associated graded \(\operatorname{gr}_{F} C\text{.}\) Each column of the \(E^{0}\) page contains a complex, one of the levels of the filtration.
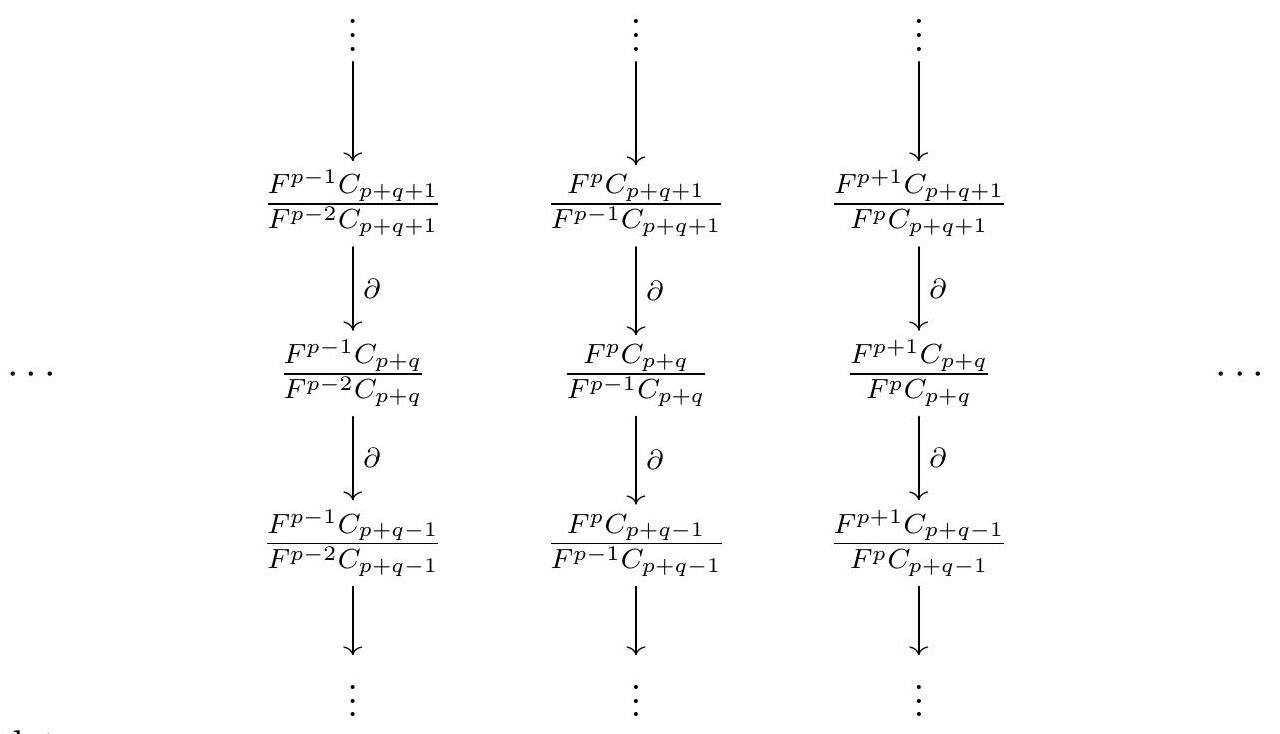
Next, let
\begin{equation*}
E_{p, q}^{1}=\mathrm{H}_{p+q}\left(G_{p} C\right)
\end{equation*}
and note that
\begin{equation*}
\mathrm{H}_{p+q}\left(G_{p} C\right)=\frac{\operatorname{ker}\left(G_{p} C_{p+q} \rightarrow G_{p} C_{p+q-1}\right)}{\operatorname{im}\left(G_{p} C_{p+q+1} \rightarrow G_{p} C_{p+q}\right)}=\frac{\operatorname{ker}\left(E_{p, q}^{0} \rightarrow E_{p, q-1}^{0}\right)}{\operatorname{im}\left(E_{p, q+1}^{0} \rightarrow E_{p, q}^{0}\right)}=\mathrm{H}_{p, q}\left(E_{\bullet, \bullet}^{0}\right)
\end{equation*}
Thus \(E_{\bullet . \bullet}^{0}\) and \(E_{\bullet \bullet}^{1}\) are consistent with being the zeroeth and first pages of a spectral sequence. Before we move on, note that we can also rewrite the \(E^{1}\) page as follows:
\begin{equation*}
E_{p, q}^{1}=\frac{\left\{x \in F^{p} C_{p+q} \mid \partial(x) \in F^{p-1} C_{p+q-1}\right\}}{F^{p-1} C_{p+q}+\partial\left(F^{p} C_{p+q+1}\right)}
\end{equation*}
One way to interpret this is that if we take an element \(x \in F^{p} C_{p+q}\) representing the class \([x] \in G_{p} C_{p+q}\) such that \(\partial([x])=0\text{,}\) then the element \(\partial(x) \in F^{p} C_{p+q-1}\) is really in \(F^{p-1} C_{p+q-1}\text{,}\) so we really should move it to the column on our left (the one indexed by \(p-1\) ).
Thus the differential on \(E_{p, q}^{1}\) is the map \(d_{1}: E_{p, q}^{1} \rightarrow E_{p-1, q}^{1}\) defined as follows: since each class \([x] \in E_{p, q}^{1}\) corresponds to an element \(x \in F^{p} C_{p+q}\) such that \(\partial(x) \in F^{p-1} C_{p+q-1}\text{,}\) we recast \(\partial(x)\) by asking about its class in \(E_{p-1, q}^{1}=F^{p-1} C_{p+q-1} / F^{p-2} C_{p+q-1}\text{.}\) If \([x] \in \operatorname{ker} d_{1}\text{,}\) that means \(\partial(x) \in F^{p-2} C_{p+q-1}\text{,}\) and so on. Ultimately, we will gather information about how deep into our filtration we can go to still find \(\partial(x)\text{.}\)
Inspired by this, we define
\begin{equation*}
E_{p, q}^{r}:=\frac{\left\{x \in F^{p} C_{p+q} \mid \partial(x) \in F^{p-r} C_{p+q-1}\right\}}{F^{p-1} C_{p+q}+\partial\left(F^{p+r-1} C_{p+q+1}\right)}
\end{equation*}
Now given \(x \in F^{p} C_{p+q}\) representing a class \([x] \in E_{p, q}^{r}\text{,}\) by definition
\begin{equation*}
\partial(x) \in F^{p-r} C_{p+q-1}
\end{equation*}
so we define
\begin{equation*}
d_{r}([x])=[\partial(x)] \in E_{p-r, q+r-1}^{r}=\frac{\left\{y \in F^{p-r} C_{p+q-1} \mid \partial(y) \in F^{p-2 r} C_{p+q-2}\right\}}{F^{p-r-1} C_{p+q-1}+\partial\left(F^{p-1} C_{p+q}\right)}
\end{equation*}
We claim that this is well-defined, and leave the details as an exercise. Moreover, \(d_{r}^{2}=0\) since \(\partial^{2}=0\text{.}\) Finally, each class in the kernel of \(d_{r}\) is represented by some \(x \in F^{p} C_{p+q}\) such that \(\partial(x) \in F^{p-r-1} C_{p+q-1}\text{,}\) while the image of \(d_{r}: E_{p+r, q-r+1}^{r} \rightarrow E_{p, q}^{r}\) consists of the image of \(\partial\left(F^{p+r} C_{p+q+1}\right)\text{.}\) Ultimately, this gives us an isomorphism
\begin{equation*}
E_{p, q}^{r+1} \cong \mathrm{H}_{p, q}\left(E^{r}\right)
\end{equation*}
Theorem 8.39. Let \((C, \partial)\) be a filtered complex with filtration \(F^{\bullet} C\text{,}\) and let
\begin{equation*}
E_{p, q}^{r}:=\frac{\left\{x \in F^{p} C_{p+q} \mid \partial(x) \in F^{p-r} C_{p+q-1}\right\}}{F^{p-1} C_{p+q}+\partial\left(F^{p+r-1} C_{p+q+1}\right)}
\end{equation*}
Then \(\partial\) induces a well-defined map
\begin{equation*}
d_{r}: E_{p, q}^{r} \rightarrow E_{p-r, q+r-1}^{r}
\end{equation*}
such that \(d_{r} d_{r}=0\text{,}\) and
\begin{equation*}
E_{p, q}^{r+1} \cong \mathrm{H}_{p, q}\left(E^{r}\right)
\end{equation*}
Thus this gives us a spectral sequence with
\begin{equation*}
E_{p, q}^{1}=\mathrm{H}_{p+q}\left(G_{p} C_{\bullet}^{\bullet}\right)
\end{equation*}
Moreover, if for all \(n\) the filtration \(F^{\bullet} C_{n}\) of \(C_{n}\) stabilizes, then the spectral sequence converges to
\begin{equation*}
E_{p, q}^{\infty}=G_{p} \mathrm{H}_{p+q}\left(C_{\bullet}\right)=F^{p} \mathrm{H}_{p+q}\left(C_{\bullet}\right) / F^{p-1} \mathrm{H}_{p+q}\left(C_{\bullet}\right)
\end{equation*}
Thus
\begin{equation*}
E_{p, q}^{\infty} \Rightarrow \mathrm{H}_{p+q}(C)
\end{equation*}
This provides a comparison between taking the homology of the associated graded module, or taking the associated graded module of the homology.
Example 8.40. Consider any short exact sequence of complexes, which we can always write as the inclusion of a subcomplex \(A\) into a complex \(B\) followed by the quotient map:
\begin{equation*}
0 \longrightarrow A \xrightarrow{i} B \stackrel{\pi}{\longrightarrow} A / B \longrightarrow 0
\end{equation*}
It turns out that we can recover the long exact sequence in homology given by the Snake Lemma via a spectral sequence. To do that, we can think of the inclusion \(A \subseteq B\) as a filtration on \(C=B\) : we set
\begin{equation*}
F^{n} C= \begin{cases}0 & \text { if } n<0 \\ A & \text { if } n=0 \\ B & \text { if } n \geqslant 1\end{cases}
\end{equation*}
Let us compute the spectral sequence of this filtered complex. First, note that In \(E^{0}\) page, we have
\begin{equation*}
E_{0, q}^{0}=F^{0} C_{q} / F^{-1} C_{q}=A_{q} \quad \text { and } \quad E_{1, q}^{0}=F^{1} C_{q+1} / F^{0} C_{q+1}=B_{q+1} / A_{q+1} \text {. }
\end{equation*}
The differential \(d^{0}\) on the \(E^{0}\) page is induced by the differential \(\partial\) on \(A\) and \(B\text{.}\) Note that we denote the differential on both complexes \(A\) and \(B\) by the same letter since the differential on \(A\) is just the restriction of the differential on \(B\text{.}\) So the \(E^{0}\) page looks like
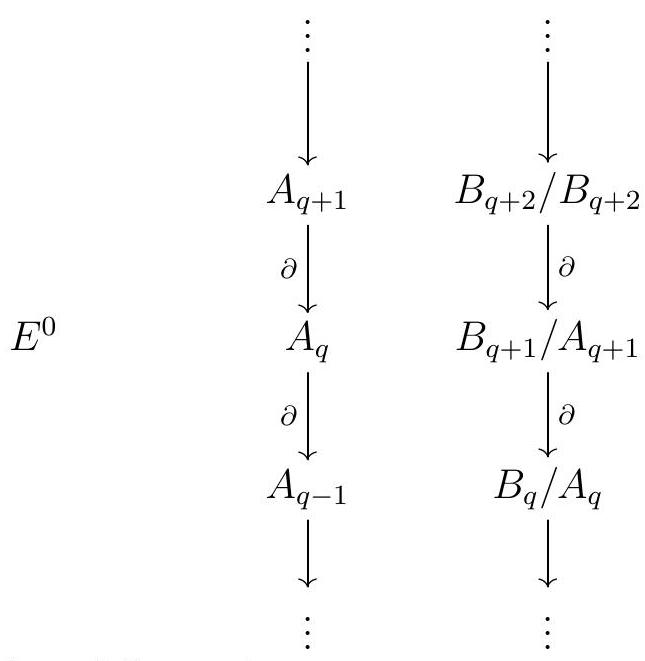
where only the 0th and first columns are nonzero.
The \(E^{1}\) page is obtained by taking homology, so it looks like
\begin{equation*}
\begin{aligned}
& \mathrm{H}_{q+1}(A) \stackrel{\partial}{\longleftarrow} \mathrm{H}_{q+2}(B / A) \\
& E^{1} \mathrm{H}_{q}(A) \stackrel{\partial}{\longleftarrow} \mathrm{H}_{q+1}(B / A) \\
& \mathrm{H}_{q-1}(A) \stackrel{\partial}{\longleftarrow} \mathrm{H}_{q}(B / A)
\end{aligned}
\end{equation*}
and the differentials \(d^{1}\text{,}\) which are now horizontal, are induced by \(\partial\text{.}\) More precisely, we can rewrite the terms on the right column as
\begin{equation*}
E_{1, q}^{1}=\mathrm{H}_{q+1}(B / A)=\frac{\left\{x \in B_{q+1} \mid \partial(x) \in A_{q}\right\}}{A_{q+1}+\partial\left(B_{q+2}\right)}
\end{equation*}
and so by definition any class \([x] \in E_{q, 1}^{1}\) is represented by some \(x \in B_{q+1}\) such that \(\partial(x) \in A_{q}\text{.}\) Since \(\partial^{2}=0\text{,}\) then \(\partial(x) \in Z_{q}(A)\text{,}\) and so we can ask about the class of \(\partial(x)\) in \(\mathrm{H}_{q}(Z)\text{.}\) So the differential \(d^{1}\) on \(E^{1}\) is given by
\begin{equation*}
\begin{aligned}
& E_{1, q}^{1}=\frac{\left\{x \in B_{q+1} \mid \partial(x) \in A_{q}\right\}}{A_{q+1}+\partial\left(B_{q+2}\right)} \longrightarrow \mathrm{H}_{q}(A) \\
& {[x] \longmapsto[\partial(x)] . }
\end{aligned}
\end{equation*}
Now onto the \(E^{2}\) page, where
\begin{equation*}
E_{1, q}^{2}=\mathrm{H}_{1, q}\left(E^{1}\right)=\operatorname{ker}\left(E_{1, q}^{1} \stackrel{d^{1}}{\longrightarrow} E_{0, q}^{1}\right)
\end{equation*}
and
\begin{equation*}
E_{0, q}^{2}=\mathrm{H}_{0, q}\left(E^{1}\right)=\mathrm{H}_{q}(A) / \operatorname{im}\left(d^{1}\right)
\end{equation*}
Note now that \(d^{2}\) is a map of degree \((-2,1)\text{,}\) and thus \(d^{2}=2\text{,}\) since we always have zero as the source or target (or both) of \(d^{2}\text{.}\) Thus \(E_{p, q}^{n}=E_{p, q}^{2}\) for all \(n \geqslant 2\text{,}\) and so by Theorem 8.39 this spectral sequence converges, with
\begin{equation*}
E_{p, q}^{\infty} \cong F^{p} \mathrm{H}_{p+q}(C) / F^{p-1} \mathrm{H}_{p+q}(C)
\end{equation*}
Now \(F^{1} \mathrm{H}_{n}(C)=\mathrm{H}_{n}(B)\text{,}\) while
\begin{equation*}
F^{0} \mathrm{H}_{n}(C)=\operatorname{im}\left(\mathrm{H}_{n}(A) \rightarrow \mathrm{H}_{n}(B)\right) \text {. }
\end{equation*}
Here the map \(\mathrm{H}(A) \rightarrow \mathrm{H}(B)\) is the map induced by the original inclusion of \(A\) into \(B\text{.}\) Moreover, \(F^{n} \mathrm{H}(C)=0\) for all \(n<0\) and \(F^{n} \mathrm{H}(C)=\mathrm{H}(B)\) for all \(n \geqslant 1\text{.}\) So for all \(n\) we get isomorphisms
\begin{equation*}
\operatorname{ker}\left(E_{1, n-1}^{1} \stackrel{d^{1}}{\longrightarrow} E_{0, n-1}^{1}\right) \cong \mathrm{H}_{n}(B) / \operatorname{im}\left(\mathrm{H}_{n}(A) \rightarrow \mathrm{H}_{n}(B)\right)=\mathrm{H}_{n}(B) / \operatorname{im~}_{n}(i)
\end{equation*}
and
\begin{equation*}
\mathrm{H}_{n}(A) / \operatorname{im}\left(d^{1}\right) \cong \operatorname{im}\left(\mathrm{H}_{n}(A) \rightarrow \mathrm{H}_{n}(B)\right)=\operatorname{im}\left(\mathrm{H}_{n}(i)\right)
\end{equation*}
So we now have all the tools we need to construct the long exact sequence in homology from this spectral sequence. First, we construct a complex. Our map \(d^{1}\) from the spectral sequence gives us homomorphisms
\begin{equation*}
\mathrm{H}_{n+1}(B / A) \stackrel{d^{1}}{\longrightarrow} \mathrm{H}_{n}(A) .
\end{equation*}
By definition, \(d^{1}([x])=[\partial(x)]\text{;}\) composing this with the map \(\mathrm{H}_{n}(i): \mathrm{H}_{n}(A) \rightarrow \mathrm{H}(B)\) consists of viewing \(\partial(x) \in Z_{n}(B / A)\) and asking for its class in \(\mathrm{H}_{n}(B)\text{.}\) But \(\partial(x) \in A_{n} \subseteq Z_{n}(B / A)\text{,}\) so the composition
\begin{equation*}
\mathrm{H}_{n+1}(B / A) \stackrel{d^{1}}{\longrightarrow} \mathrm{H}_{n}(A) \stackrel{\mathrm{H}_{n}(i)}{\longrightarrow} \mathrm{H}_{n}(B)
\end{equation*}
is zero.
Similarly, the map \(\mathrm{H}_{n+1}(B) \rightarrow \mathrm{H}_{n+1}(A)\) takes a class \([y] \in \mathrm{H}_{n}(B)\text{,}\) represented by \(y \in\) \(Z_{n}(B)\text{,}\) and identifies \(y\) with its image in \(Z_{n}(B) \subseteq Z_{n}(B / A)\text{.}\) But \(\partial(y)=0\) by definition, so \([\partial(y)]=0\) and the composition
\begin{equation*}
\begin{array}{r}
\mathrm{H}_{n+1}(B) \longrightarrow \mathrm{H}_{n+1}(B / A) \stackrel{d^{1}}{\longrightarrow} \mathrm{H}_{n}(A) \\
\quad[y] \longmapsto[y] \longmapsto[\partial(y)]
\end{array}
\end{equation*}
is the zero map. Moreover, \(\mathrm{H}_{n}\) is an additive functor, and thus it takes \(A \rightarrow B \rightarrow B / A\) to a complex, so putting it all together we get a complex
\begin{equation*}
\mathrm{H}_{n+1}(B / A) \stackrel{d^{1}}{\longrightarrow} \mathrm{H}_{n}(A) \stackrel{\mathrm{H}_{n}(i)}{\longrightarrow} \mathrm{H}_{n}(B) \stackrel{\mathrm{H}_{n}(\pi)}{\longrightarrow} \mathrm{H}_{n}(B / A) \xrightarrow{d^{1}} \mathrm{H}_{n-1}(A)
\end{equation*}
All that is left is for us to check that exactness follows from our spectral sequence. On the one hand, the fact that this is a complex says that
\begin{equation*}
\operatorname{im}\left(d^{1}\right) \subseteq \operatorname{ker}\left(\mathrm{H}_{n}(i)\right)
\end{equation*}
but our spectral sequence gave us the isomorphism
\begin{equation*}
\mathrm{H}_{n}(A) / \operatorname{im}\left(d^{1}\right) \cong \operatorname{im}\left(\mathrm{H}_{n}(i)\right)
\end{equation*}
so by the First Isomorphism Theorem we get
\begin{equation*}
\mathrm{H}_{n}(A) / \operatorname{ker}\left(\mathrm{H}_{n}(i)\right) \cong \operatorname{im}\left(\mathrm{H}_{n}(i)\right) \cong \mathrm{H}_{n}(A) / \operatorname{im}\left(d^{1}\right)
\end{equation*}
We can now conclude that \(\operatorname{im}\left(d^{1}\right)=\operatorname{ker} \mathrm{H}_{n}(i)\text{.}\) This gives us exactness at \(\mathrm{H}_{n}(A)\text{.}\) Similarly, we claim that the fact that we have a complex gives us a map
\begin{equation*}
\begin{gathered}
\operatorname{coker}\left(\mathrm{H}_{n}(i)\right) \stackrel{\psi}{\longrightarrow} \operatorname{ker}\left(d^{1}\right) \\
x+\operatorname{im}\left(\mathrm{H}_{n}(i)\right) \longmapsto \mathrm{H}_{n}(\pi)(x) .
\end{gathered}
\end{equation*}
Indeed, for any \(x \in \mathrm{H}_{n}(B)\) we get \(\mathrm{H}_{n}(\pi)(x) \in \operatorname{ker} d^{1}\text{,}\) and the map is well-defined since if \(x \in \operatorname{im}\left(\mathrm{H}_{n}(i)\right) \subseteq \operatorname{ker}\left(\mathrm{H}_{n}(\pi)\right)\) then by definition \(\mathrm{H}_{n}(\pi)(x)=0\text{,}\) so that we get a well-defined map from \(\operatorname{coker}\left(\mathrm{H}_{n}(i)\right)\text{.}\) But our spectral sequence gave us an isomorphism
\begin{equation*}
\operatorname{ker}\left(d^{1}\right) \cong \mathrm{H}_{n}(B) / \operatorname{im}\left(\mathrm{H}_{n}(i)\right)=\operatorname{coker}\left(\mathrm{H}_{n}(i)\right)
\end{equation*}
so that the map \(\psi\) we defined above is an isomorphism, and thus we must have
\begin{equation*}
\operatorname{ker}\left(\mathrm{H}_{n}(\pi)\right)=\operatorname{im}\left(\mathrm{H}_{n}(i)\right)
\end{equation*}
proving exactness at \(\mathrm{H}_{n}(B)\text{.}\)
Finally, this also says that we can rewrite our previous isomorphism as
\begin{equation*}
\operatorname{ker}\left(d^{1}\right) \cong \mathrm{H}_{n}(B) / \operatorname{im}\left(\mathrm{H}_{n}(i)\right)=\mathrm{H}_{n}(B) / \operatorname{ker}\left(\mathrm{H}_{n}(\pi)\right)
\end{equation*}
but by the First Isomorphism Theorem we get
\begin{equation*}
\operatorname{ker}\left(d^{1}\right) \cong \operatorname{im}\left(\mathrm{H}_{n}(\pi)\right)
\end{equation*}
We already knew that \(\operatorname{im}\left(\mathrm{H}_{n}(\pi)\right) \subseteq \operatorname{ker}\left(d^{1}\right)\) from the fact that we had a complex, so we conclude that we must have exactness at \(\mathrm{H}_{n}(B / A)\text{.}\)
Thus we have recovered the connecting homomorphism from the Snake Lemma and the long exact sequence in homology, all via this spectral sequence.
