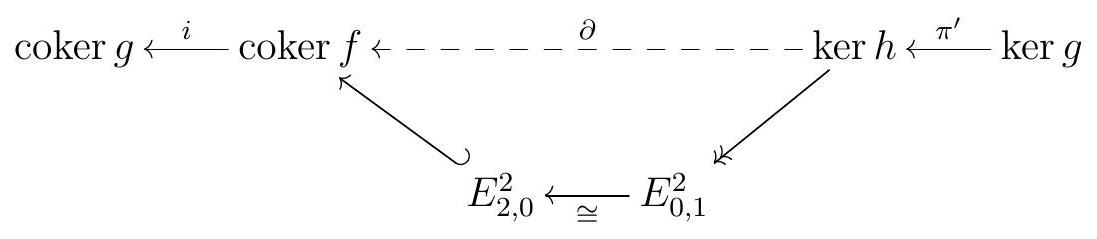Section 7.4 Double Complexes
One important example of a spectral sequence induced by a filtered complex is the case of the spectral sequence of a double complex.
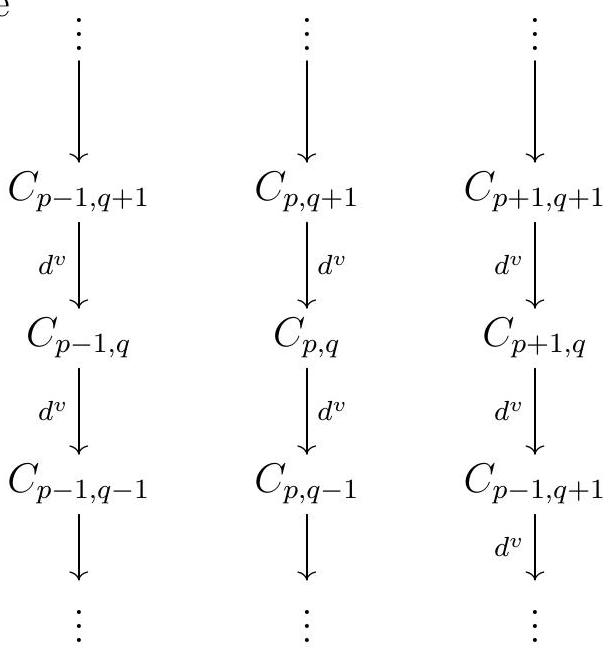
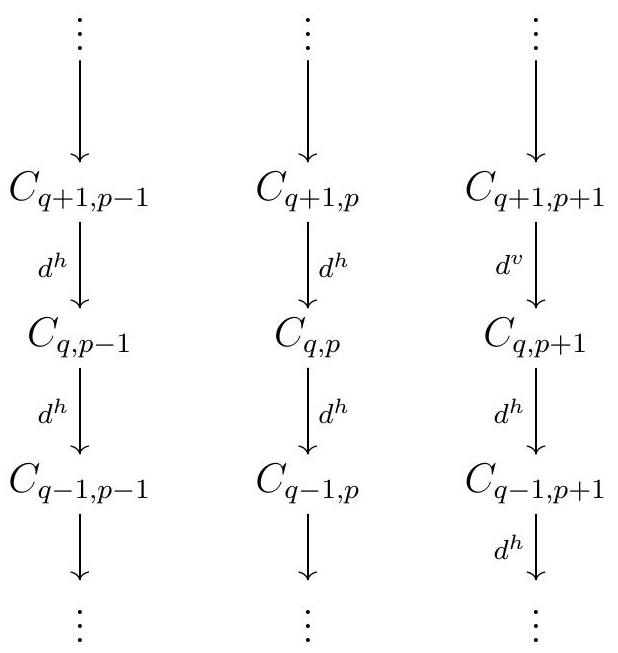
Definition 8.41. Let \(C\) be a double complex. There are two canonical filtrations on the total complex of \(C\) :
(I) The First Filtration of \(\operatorname{Tot}^{\oplus}(C)\) is the filtration \({ }^{I} F^{s} \operatorname{Tot}^{\oplus}(C)\) given by
\begin{equation*}
{ }^{I} F^{s} \operatorname{Tot}^{\oplus}(C)_{n}:=\bigoplus_{i \leqslant s} C_{i, n-i}
\end{equation*}
For each \(s,{ }^{I} F^{s} \operatorname{Tot}^{\oplus}(C)\) is the subcomplex of \(\operatorname{Tot}^{\oplus}(C)\) obtained by first truncating \(C\) at \(p=s\) :
The First Filtration
II The Second Filtration of \(\operatorname{Tot}^{\oplus}(C)\) is the filtration \({ }^{I I} F^{s} \operatorname{Tot}^{\oplus}(C)\) given by
\begin{equation*}
{ }^{I I} F^{s} \operatorname{Tot}^{\oplus}(C)_{n}:=\bigoplus_{j \leqslant s} C_{n-j, j}
\end{equation*}
For each \(s,{ }^{I I} F^{s} \operatorname{Tot}^{\oplus}(C)\) is the subcomplex of \(\operatorname{Tot}^{\oplus}(C)\) obtained by truncating \(C\) at \(q=s\) :
The Second Filtration
Each of these filtered complexes gives rise to a spectral sequence.
Discussion 8.42 (First Spectral Sequence). Let us examine the spectral sequence induced by the First Filtration, which we write as \({ }^{I} E^{s}\text{.}\) To make the notation less heavy, we will write
\begin{equation*}
E_{p, q}^{r}:={ }^{I} E_{p, q}^{r} \quad \text { and } F^{p}:={ }^{I} F^{s} \operatorname{Tot}^{\oplus}(C) \quad \text { so } \quad F_{n}^{p}=\bigoplus_{i \leqslant s} C_{i, n-i}
\end{equation*}
Our spectral sequence starts with
\begin{equation*}
E_{p, q}^{0}=F_{p+q}^{p} / F_{p+q}^{p-1}=\bigoplus_{i \leqslant p} C_{i, p+q-i} / \bigoplus_{i \leqslant p-1} C_{i, p+q-i}=C_{p, q}
\end{equation*}
so that
\begin{equation*}
E_{p, \bullet}^{0}=C_{p, \bullet}=p \text { th column of } C
\end{equation*}
Moreover,
\begin{equation*}
d_{0}: C_{p, q}=E_{0}^{p, q} \longrightarrow E_{0}^{p, q-1}=C_{p, q-1}
\end{equation*}
is the map induced by the differential \(d=d^{v}+d^{h}\) on this filtration. Since
\begin{equation*}
d: C_{p, q} \stackrel{\left(d^{h}, d^{v}\right)}{\longrightarrow} C_{p-1, q} \oplus C_{p, q-1}
\end{equation*}
we conclude that \(d_{0}\) is precisely the vertical differential \(d^{v}\) of the original double complex \(C\text{.}\) Thus the \(E_{0}\) page looks like \(E^{0}\)
Then \(E_{p, q}^{1}=\mathrm{H}_{q}^{v}\left(C_{p, \bullet}\right)\text{,}\) and
\begin{equation*}
d_{1}: \mathrm{H}_{q}^{v}\left(C_{p, \bullet}\right)=E_{p, q}^{1} \longrightarrow E_{p-1, q}^{1}=\mathrm{H}_{q}^{v}\left(C_{p-1, \bullet}\right)
\end{equation*}
is the map induced by \(d: C_{p, q} \stackrel{\left(d^{h}, d^{v}\right)}{\longrightarrow} C_{p-1, q} \oplus C_{p, q-1}\text{.}\) This is the horizontal differential \(d^{h}\text{.}\) We conclude that
\begin{equation*}
{ }^{I} E_{p, q}^{2}=\mathrm{H}_{p}^{h} \mathrm{H}_{q}^{v}(C)
\end{equation*}
We automatically get a convergence theorem from Theorem 8.39.
Theorem 8.43. If \(C\) is a bounded double complex, then
\begin{equation*}
{ }^{I} E_{p, q}^{2} \Rightarrow \mathrm{H}_{p+q}\left(\operatorname{Tot}^{\oplus}(C)\right)
\end{equation*}
Discussion 8.44 (Second Spectral Sequence). Let us examine the spectral sequence induced by the Second Filtration, which we write as \({ }^{I I} E^{s}\text{.}\) To make the notation less heavy, we will write
Our spectral sequence starts with
\begin{equation*}
F^{p}:={ }^{I I} F^{s} \operatorname{Tot}^{\oplus}(C) \quad \text { so } \quad F_{n}^{p}=\bigoplus_{j \leqslant s} C_{n-j, j}
\end{equation*}
\begin{equation*}
E_{p, q}^{0}=F_{p+q}^{p} / F_{p+q}^{p-1}=\bigoplus_{j \leqslant p} C_{p+q-j, j} / \bigoplus_{j \leqslant p-1} C_{p+q-j, j}=C_{q, p}
\end{equation*}
so that
\begin{equation*}
E_{p, \bullet}^{0}=C_{\bullet, p}=p \text { th column of } C \text {. }
\end{equation*}
Moreover,
\begin{equation*}
d_{0}: C_{q, p}=E_{p, q}^{0} \longrightarrow E_{p, q-1}^{0}=C_{q-1, p}
\end{equation*}
is the map induced by the differential \(d=d^{v}+d^{h}\) on this filtration. Since
\begin{equation*}
d: C_{p, q} \stackrel{\left(d^{h}, d^{v}\right)}{\longrightarrow} C_{p-1, q} \oplus C_{p, q-1}
\end{equation*}
we conclude that \(d_{0}\) is precisely the horizontal differential \(d^{h}\) of the original double complex \(C\text{.}\) Thus the \(E_{0}\) page looks like
Then \(E_{p, q}^{1}=\mathrm{H}_{q}^{h}\left(C_{\bullet, p}\right)\text{,}\) and
\begin{equation*}
d_{1}: \mathrm{H}_{q}^{h}\left(C_{\bullet, p}\right)=E_{p, q}^{1} \longrightarrow E_{p-1, q}^{1}=\mathrm{H}_{q}^{h}\left(C_{\bullet, p-1}\right)
\end{equation*}
is the map induced by \(d: C_{p, q} \stackrel{\left(d^{h}, d^{v}\right)}{\longrightarrow} C_{p-1, q} \oplus C_{p, q-1}\text{.}\) Thus \(d_{1}\) is the vertical differential \(d^{v}\text{.}\) We conclude that
\begin{equation*}
{ }^{I I} E_{p, q}^{2}=\mathrm{H}_{p}^{v} \mathrm{H}_{q}^{h}(C)
\end{equation*}
We now get a convergence theorem automatically from Theorem 8.39.
Theorem 8.45. If \(C\) is a bounded double complex, then
\begin{equation*}
{ }^{I I} E_{p, q}^{2} \Rightarrow \mathrm{H}_{p+q}\left(\operatorname{Tot}^{\oplus}(C)\right)
\end{equation*}
Remark 8.46. We know exactly how each spectral sequence converges to \(\mathrm{H}_{n}\left(\operatorname{Tot}^{\oplus}(C)\right)\) : via the filtration on \(\mathrm{H}_{n}\left(\operatorname{Tot}^{\oplus}(C)\right)\) induced by the given filtration on \(\operatorname{Tot}^{\oplus}(C)\text{.}\) More precisely,
\begin{equation*}
{ }^{I} E_{p, q}^{\infty}=\frac{{ }^{I} F^{p} \mathrm{H}_{p+q}\left(\operatorname{Tot}^{\oplus}(C)\right)}{{ }^{I} F^{p-1} \mathrm{H}_{p+q}\left(\operatorname{Tot}^{\oplus}(C)\right)} \quad \text { and } \quad{ }^{I I} E_{p, q}^{\infty}=\frac{{ }^{I I} F^{p} \mathrm{H}_{p+q}\left(\operatorname{Tot}^{\oplus}(C)\right)}{{ }^{I I} F^{p-1} \mathrm{H}_{p+q}\left(\operatorname{Tot}^{\oplus}(C)\right)}
\end{equation*}
Remark 8.47. If \(C\) is a first quadrant double complex, so that \(C_{i, j}=0\) whenever \(i<0\) or \(j<0\text{,}\) then for all \(p<0\) we have
\begin{equation*}
{ }^{I} F^{p} \operatorname{Tot}^{\oplus}(C)=0 \text { and }{ }^{I I} F^{p} \operatorname{Tot}^{\oplus}(C)=0
\end{equation*}
Thus
\begin{equation*}
{ }^{I} F^{p} \mathrm{H}\left(\operatorname{Tot}^{\oplus}(C)\right)=0 \text { and }{ }^{I I} F^{p} \mathrm{H}\left(\operatorname{Tot}^{\oplus}(C)\right)=0 \text {. }
\end{equation*}
Moreover, for each fixed \(n\) if we take \(p>n\) or \(q>n\) then
\begin{equation*}
{ }^{I} F^{p} \operatorname{Tot}^{\oplus}(C)_{n}=\operatorname{Tot}^{\oplus}(C)_{n} \text { and }{ }^{I I} F^{p} \operatorname{Tot}^{\oplus}(C)_{n}=\operatorname{Tot}^{\oplus}(C)_{n}
\end{equation*}
so
\begin{equation*}
{ }^{I} F^{p} \mathrm{H}_{n}\left(\operatorname{Tot}^{\oplus}(C)\right)=\mathrm{H}_{n}\left(\operatorname{Tot}^{\oplus}(C)\right) \text { and }{ }^{I I} F^{p} \mathrm{H}_{n}\left(\operatorname{Tot}^{\oplus}(C)\right)=\mathrm{H}_{n}\left(\operatorname{Tot}^{\oplus}(C)\right) \text {. }
\end{equation*}
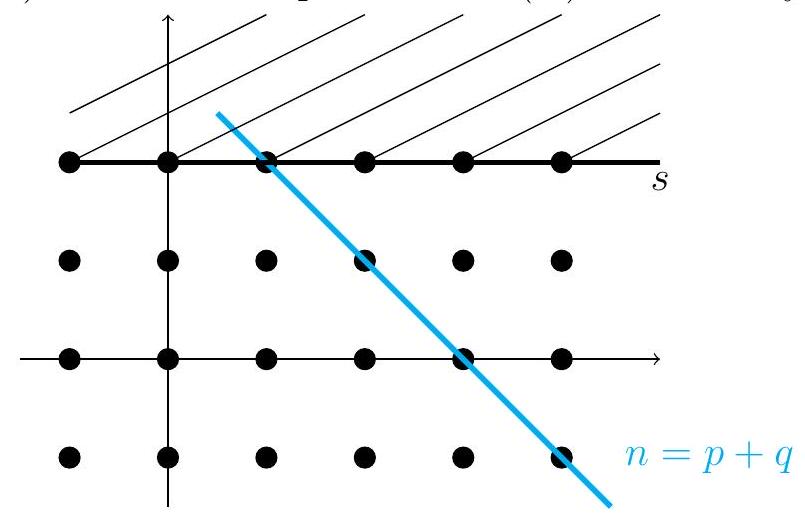
Thus each fixed diagonal of \({ }^{I} E_{\infty}^{p, q}\) and \({ }^{I I} E_{2}^{p, q}\) contains the factors of a finite filtration on \(\mathrm{H}_{n}\left(\operatorname{Tot}^{\oplus}(C)\right)\) :
\begin{equation*}
0=M_{0} \subseteq M_{1} \subseteq \cdots \subseteq M_{s}=\mathrm{H}_{n}\left(\operatorname{Tot}^{\oplus}(C)\right)
\end{equation*}
In the special case when \({ }^{I} E\) or \({ }^{I I} E\) collapses, meaning that \(E^{\infty}\) is concentrated in one row or column, then the filtration on \(\mathrm{H}\left(\operatorname{Tot}^{\oplus}(C)\right)\) has a unique term in each degree, so that we can read \(\mathrm{H}\left(\operatorname{Tot}^{\oplus}(C)\right)\) exactly from the \(E^{\infty}\) page.
Remark 8.48. The fact that \({ }^{I I} E_{p, q}^{0}=C_{q, p}\) can lead to a lot of confusion. To make things easier, one often breaks the rules a little and instead takes the \(E_{0}\) page to be \({ }^{I I} E_{p, q}^{0}=C_{p, q}\) with horizontal differentials, the \(E^{1}\) page to have vertical differentials induced by the vertical differentials on \(C\text{,}\) and then the \(E^{r}\) page to have a differential of degree \((r-1,-r)\text{.}\) This gives us a gadget that isn’t quite a spectral sequence under our formal definition, but should be a spectral sequence. In fact, this new convention makes everything much easier to read.
Under this reasonable convention, the differentials look as follows:
0th page
1st page
2nd page
Also, note that now
\begin{equation*}
{ }^{I I} E_{p, q}^{2}=\mathrm{H}_{q}^{v} \mathrm{H}_{p}^{h}(C)
\end{equation*}
and that while
\begin{equation*}
{ }^{I I} E_{p, q}^{\infty} \Longrightarrow \mathrm{H}_{p+q}\left(\operatorname{Tot}^{\oplus}(C)\right)
\end{equation*}
we now should carefully read the filtration backwards:
\begin{equation*}
{ }^{I I} E_{p, q}^{\infty}=\frac{F^{q} \mathrm{H}_{p+q}\left(\operatorname{Tot}^{\oplus}(C)\right)}{F^{q-1} \mathrm{H}_{p+q}\left(\operatorname{Tot}^{\oplus}(C)\right)}
\end{equation*}
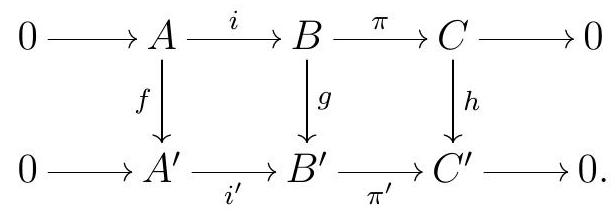
Example 8.49. Let us give a new proof of the Snake Lemma using spectral sequences. More precisely, we will show that given any commutative diagram with exact rows
then there exists an exact sequence
\begin{equation*}
0 \longrightarrow \operatorname{ker} f \longrightarrow \operatorname{ker} g \longrightarrow \operatorname{ker} h \stackrel{\partial}{\longrightarrow} \operatorname{coker} f \longrightarrow \operatorname{coker} g \longrightarrow \text { coker } h \longrightarrow 0
\end{equation*}
To do that, we start by viewing our commutative diagram as a double complex \(M\text{,}\) as follows: we set \(M_{0,0}=C, M_{0,1}=C^{\prime}\text{,}\) and so on, resulting in
Now notice that \(M\) is a first quadrant double complex with exact rows, so by the Acyclic Assembly Lemma, \(\operatorname{Tot}^{\oplus}(M)\) is exact. We can also prove that \(\operatorname{Tot}^{\oplus}(M)\) is exact by computing the spectral sequence arising from the Second Filtration on \(M\text{,}\) which under our new and improved notation from Remark 8.48 has
\begin{equation*}
\begin{aligned}
& C \stackrel{\pi}{\longleftarrow} B \stackrel{i}{\longleftarrow} C \\
& E^{0}= \\
& C^{\prime} \underset{\pi^{\prime}}{\longleftarrow} B^{\prime} \underset{i^{\prime}}{\longleftarrow} C^{\prime}
\end{aligned}
\end{equation*}
and since the rows are all exact, we see that in the next step we will end up with \(E^{1}=0\text{,}\) and thus \(E^{\infty}=0\text{.}\) Therefore, \(\mathrm{H}\left(\operatorname{Tot}^{\oplus}(M)\right)=0\text{.}\)
Now consider the spectral sequence induced by the First Filtration on \(M\text{,}\) which has
Now whatever \(E^{2}\) is, since \(d^{2}\) is a \((-2,1)\) degree map, the only possible nonzero differential on \(E^{2}\) is \(d^{2}: E_{2,0}^{2} \rightarrow E_{0,1}^{2}\text{.}\) Moreover, all the differentials on all the higher pages vanish, simply because there are not enough nonzero modules already, so \(E^{3}=E^{\infty}\text{.}\) But we know that \(\operatorname{Tot}^{\oplus}(M)\) is exact, so in fact since our filtrations are finite we must necessarily have \(E^{\infty}=0\text{.}\) In particular, the only potentially nonzero objects in \(E^{2}\) are \(E_{0,1}^{2}\) and \(E_{2,0}^{2}\text{,}\) so this proves the exactness of
Moreover, the fact that \(E_{0,1}^{2}\) and \(E_{2,0}^{2}\) are the only possible nonzero objects in \(E^{2}\) together with the fact that and \(E_{0,1}^{3}=0=E_{2,0}^{3}\) imply that \(d^{2}: E_{0,1}^{2} \rightarrow E_{2,10}^{2}\) must be an isomorphism. More precisely, we get an isomorphism
\begin{equation*}
\operatorname{coker}\left(\operatorname{ker} h \stackrel{\pi^{\prime}}{\longleftarrow} \operatorname{ker} g\right)=E_{0,1}^{2} \cong E_{2,0}^{2}=\operatorname{ker}(\operatorname{coker} g \stackrel{i}{\longleftarrow} \operatorname{coker} f) .
\end{equation*}
Thus we get an exact sequence
where the map \(\partial\) obtained by composition is the connecting homomorphism we dreamed of.
Exercise 7.39.
Exercise 96. Show that if \(M\) is a first quadrant double complex with exact rows or exact columns, then \(\operatorname{Tot}^{\oplus}(M)\) is exact.
Exercise 7.40.
Exercise 97. Let \(M\) and \(N\) be \(R\)-modules and fix projective resolutions \(P\) for \(M\) and \(Q\) for \(N\text{.}\) Consider the double complex \(C=P \otimes_{R} Q\text{.}\)
a) Compute the spectral sequence associated to the First Filtration (I) on \(C\) up to the \(E^{2}\) page.
b) Compute the spectral sequence associated to the Second Filtration II on \(C\) up to the \(E^{2}\) page.
c) Give a new proof that Tor is balanced:
\begin{equation*}
\mathrm{H}_{n}\left(P \otimes_{R} N\right) \cong \mathrm{H}_{n}\left(M \otimes_{R} Q\right) .
\end{equation*}
Exercise 7.41.
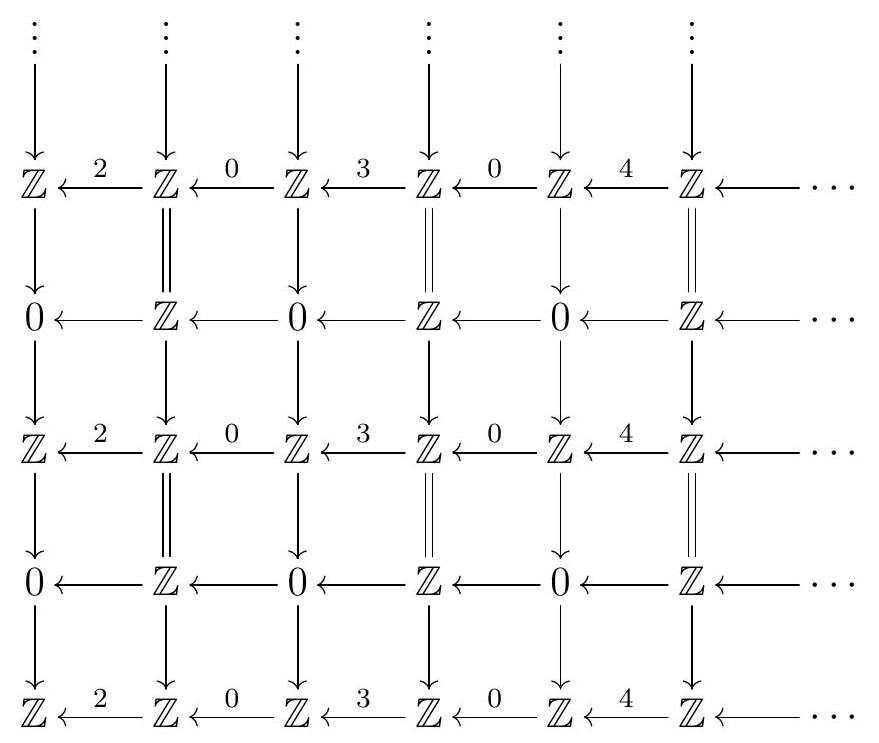
Exercise 98. Consider the following first quadrant double complex \(C\) :
a) Compute the spectral sequence associated to the First Filtration (I) until it stabilizes.
b) Compute the spectral sequence associated to the Second Filtration II until it stabilizes.
c) How are the two resulting \(E^{\infty}\) pages even possible considering they both converge to the same thing?
d) Compute \(\mathrm{H}_{3}\left(\operatorname{Tot}^{\oplus}(M)\right)\) explicitly using only the two spectral sequences you calculated.
e) Check your work by computing \(\mathrm{H}_{3}\left(\operatorname{Tot}^{\oplus}(M)\right)\) explicitly from the definition of \(\operatorname{Tot}^{\oplus}(M)\text{.}\)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)