Skip to main content

Postmodern Algebra

Sam Macdonald

Section 3.1 Projective Modules

Subsection Definition, Free Modules are Projective

“I don’t have time to worry about what I’m projecting to the world. I’m just busy being myself.”
―Demi Lovato
While Hom and tensor are not exact functors in general, \(\operatorname{Hom}_{R}(M,-), \operatorname{Hom}_{R}(-, M)\text{,}\) and \(M \otimes_{R}-\) can be exact functors for carefully chosen modules \(M\text{.}\) In this chapter, we introduce these three classes of modules (projective, injective, and flat modules) and study their properties. Throughout, we consider general rings and left modules.

Definition 3.1. Projective Module.

Let \(R\) be a ring. An \(R\)-module \(P\) is projective if given any surjective \(R\)-module homomorphism \(s: A \rightarrow B\) and any \(R\)-module homomorphism \(f: P \rightarrow B\text{,}\) there exists an \(R\)-module homomorphism \(g\) such that the diagram
commutes.

Remark 3.2.

The commutativity of the diagram
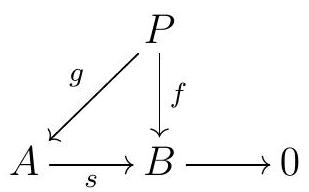
says that \(s_{*}(g)=f\text{,}\) where \(s_{*}\) is the \(\operatorname{map} \operatorname{Hom}_{R}(P, A) \longrightarrow \operatorname{Hom}_{R}(P, B)\) induced by \(s\text{.}\) Whenever this happens, we say that \(g\) is a lifting of \(f\text{,}\) and that \(f\) lifts, or that \(f\) factors through \(A\text{.}\)
There are projective modules over any ring, as the next result shows; in fact, free modules are always projective.

Proof.

Let \(F\) be a free \(R\)-module. Suppose we are given \(R\)-module homomorphisms \(s: A \rightarrow C\) and \(f: F \rightarrow C\) such that \(s\) is surjective. Fix a basis \(B=\left\{b_{i}\right\}_{i}\) for \(F\text{.}\) Since \(s\) is surjective, for each \(i\) we can choose \(a_{i} \in A\) such that \(s\left(a_{i}\right)=f\left(b_{i}\right)\text{.}\) Consider the function \(u: B \longrightarrow A\) given by \(u\left(b_{i}\right)=a_{i}\text{.}\) The universal property of free modules says that there exists an \(R\)-module homomorphism \(g: F \longrightarrow A\) that coincides with \(u\) for all basis elements. Now
\begin{equation*} s g\left(b_{i}\right)=s u\left(b_{i}\right)=s\left(a_{i}\right)=f\left(b_{i}\right) \end{equation*}
so \(s g\) agrees with \(f\) for all basis elements. Since \(B\) generates \(F\text{,}\) we conclude that \(s g=f\text{.}\)
Projective modules are precisely those that make the covariant \(\Hom\) functor exact.

Proof.

By Theorem 2.25 \(\operatorname{Hom}_{R}(P,-)\) is left exact. The statement is that \(P\) is projective if and only for any short exact sequence
\begin{equation*} 0 \longrightarrow A \stackrel{i}{\longrightarrow} B \stackrel{p}{\longrightarrow} C \longrightarrow 0 \end{equation*}
the induced map \(s_{*}: \operatorname{Hom}_{R}(P, B) \longrightarrow \operatorname{Hom}_{R}(P, C)\) is surjective. Say we are given a surjective map
\begin{equation*} B \stackrel{p}{\longrightarrow} C \longrightarrow 0 \end{equation*}
The induced map \(s_{*}\) is surjective if and only if for every \(f \in \operatorname{Hom}_{R}(P, C)\) there exists a lifting \(g \in \operatorname{Hom}_{R}(P, B)\) of \(f\text{,}\) meaning \(s_{*}(g)=f\text{.}\) By Remark 3.2, the existence of such a \(g\) for all such surjective maps \(s\) is precisely the condition that \(P\) is projective.

Proof.

By Theorem 3.3, free modules, and \(R\) in particular, are projective. By Theorem 3.4, \(\operatorname{Hom}_{R}(F,-)\) must be exact for any free \(R\)-module \(F\text{.}\)
However, not every projective module is free. But before we see such examples, we need to know a bit more about projective modules.

Subsection Direct Summands

“”
―
First, we show that we can rephrase the condition that a module is projective or injective in terms of split exact sequences.

Proof.

\((\Rightarrow)\) Consider a short exact sequence
\begin{equation*} 0 \longrightarrow A \stackrel{f}{\longrightarrow} B \stackrel{g}{\longrightarrow} P \longrightarrow 0 . \end{equation*}
If \(P\) is projective, the identity map on \(P\) lifts to a map \(P \longrightarrow B\text{,}\) meaning that
commutes. This says that our map \(h\)
\begin{equation*} 0 \longrightarrow A \stackrel{f}{\longrightarrow} B \underset{\nwarrow}{\stackrel{g}{\longrightarrow}} P \longrightarrow 0 \end{equation*}
is a splitting for our short exact sequence, which must then be split, by Lemma 2.19.
\((\Leftarrow)\) Conversely, suppose that every short exact sequence
\begin{equation*} 0 \longrightarrow A \longrightarrow B \longrightarrow P \longrightarrow 0 \end{equation*}
splits, and consider any diagram
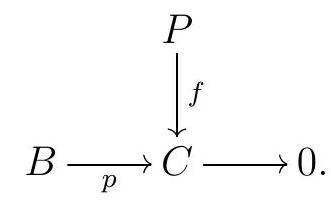
Let \(F\) be a free module that surjects onto \(P\) - for example, the free module on a set of generators of \(P\) - and fix a surjection \(\pi: F \rightarrow P\text{.}\) By assumption, the short exact sequence
\begin{equation*} 0 \longrightarrow \operatorname{ker} \pi \longrightarrow \underset{\kappa_{h}^{-}}{\stackrel{\pi}{\longrightarrow}} P \longrightarrow 0 \end{equation*}
splits, so by Lemma 1.51 there exists \(h\) such that \(\pi h=\operatorname{id}_{P}\text{.}\) Now since \(F\) is free, we can define an \(R\)-module map \(\hat{g}: F \longrightarrow B\) that such that
commutes, by sending each basis element \(b \in F\) to any lift of \(f \pi(b)\) in \(B\) via \(s\text{.}\) Now set \(g:=\hat{g} h\text{,}\) and note that
\begin{equation*} \begin{array}{rrr} s g & =s \hat{g} h & \text { by definition } \\ & =f \pi h & \text { by commutativity } \\ & =f & \text { since } \pi h=\mathrm{id}_{P}, \end{array} \end{equation*}
so \(g\) is a lift of \(s\) by \(f\text{.}\)
We have seen that free modules are projective; what other modules are projective?

Definition 3.7. Direct Summand.

An \(R\)-module \(M\) is a direct summand of an \(R\)-module \(N\) if there exists an \(R\)-module \(A\) such that \(A \oplus M \cong N\text{.}\)

Remark 3.8.

Remark 4.8. Saying that \(M\) is a direct summand of \(N\) is equivalent to giving a splitting \(\pi\) of the inclusion map \(i: M \hookrightarrow N\text{,}\) meaning that \(\pi i=\mathrm{id}_{N}\text{.}\) As we have argued in Lemma 1.51, such a splitting \(\pi\) gives
\begin{equation*} N=\operatorname{im} i \oplus \operatorname{ker} \pi \end{equation*}
Essentially repeating the argument we used in Lemma 1.51, every element in \(N\) can be written as
\begin{equation*} n=(n-i \pi(n))+i \pi(n) \end{equation*}
where \(i \pi(n) \in \operatorname{im} i\) and \(n-i \pi(n) \in \operatorname{ker} \pi\text{,}\) and \(\operatorname{ker} \pi \cap \operatorname{im} i=0\) because if \(i(a) \in \operatorname{ker} \pi\) then \(a=\pi i(a)=0\text{.}\)
Note that when we are dealing with graded modules over a graded ring, the kernels and images of graded maps are graded modules, and the equality \(N=\operatorname{im} i \oplus \operatorname{ker} \pi\) is a graded direct sum of graded modules.

Proof.

\((\Rightarrow)\) Let \(P\) be a projective module, and fix a free module \(F\) surjecting onto \(P\text{.}\) If \(P\) is finitely generated, we can take \(F=R^{n}\) for some \(n\text{.}\) The short exact sequence
\begin{equation*} 0 \longrightarrow \operatorname{ker} \pi \longrightarrow F \stackrel{\pi}{\longrightarrow} P \longrightarrow 0 \end{equation*}
must split by Theorem 3.6, so \(P\) is a direct summand of \(F\text{.}\)
\((\Leftarrow)\) Now suppose \(P\) is a direct summand of a free module \(F\text{.}\) In particular, we have an inclusion map \(i: P \longrightarrow F\) that splits, so it comes together with a projection map \(\pi: F \longrightarrow P\) such that \(\pi i=\operatorname{id}_{P}\text{.}\) Given any diagram
we can define an \(R\)-module homomorphism \(h\) such that \(s h=f \pi\text{,}\) so that the following diagram commutes:
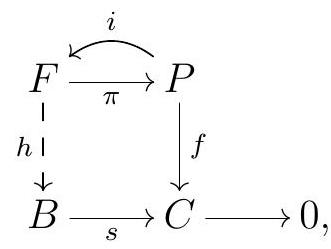
Setting \(g:=h i\text{,}\) we do indeed obtain \(s g=f\text{,}\) since
\begin{equation*} \begin{array}{rlrl} s g & =s h i & \text { by definition } \\ & =f \pi i & & \text { because } s h=f \pi \\ & =f & & \text { since } \pi i=\mathrm{id}_{P} \cdot \square \end{array} \end{equation*}

Remark 3.10.

Remark 4.10. While every module \(M\) is a quotient of a free module \(F\text{,}\) so that we always have a surjection \(\pi: F \rightarrow M\text{,}\) not every module embeds into a free module; and even if \(M\) is a submodule of some free module \(F\text{,}\) the inclusion map \(M \subseteq F\) is not necessarily split. On the other hand, as we showed in Theorem 3.9 that \(M\) is projective if and only if we can write it as a quotient of a free module \(F\text{,}\) say \(\pi: F \rightarrow M\text{,}\) and \(\pi\) splits, so that in fact \(M\) embeds into \(F\) and that map splits.

Proof.

  1. Suppose \(M \oplus A \cong P\) for some projective module \(P\text{.}\) By Theorem 3.9, there exists a free \(R\)-module \(F\) and an \(R\)-module \(B\) such that \(P \oplus B \cong F\text{.}\) Then \(M \oplus A \oplus B \cong P \oplus B \cong F\text{,}\) and by Theorem 3.9 this implies \(M\) is projective.
  2. Let \(\left\{P_{i}\right\}_{i \in I}\) be a family of projective modules. By Theorem 3.9, there exist free modules \(F_{i}\) such that each \(P_{i}\) is a direct summand of \(F_{i}\text{.}\) Therefore, \(\oplus P_{i}\) is a direct summand of \(\oplus_{i} F_{i}\text{,}\) which is also free. By Theorem 3.9, this implies that \(\oplus P_{i}\) is projective.
We are finally ready to give examples showing that projective modules are not necessarily free.

Example 3.12. Projective but not Free Module.

Example 4.12. The ring \(R=\mathbb{Z} /(6)\) can be written as a direct sum of the ideals
\begin{equation*} I=(2) \text { and } J=(3) \end{equation*}
Indeed, \(R=I+J\) and \(I \cap J=0\text{,}\) so \(R=I \oplus J\text{.}\) By Corollary 3.11, \(I\) and \(J\) are projective \(R\)-modules. However, \(I\) and \(J\) are not free. This can be explained numerically: every finitely generated free \(R\)-module is of the form \(R^{n}\text{,}\) so it has \(6^{n}\) elements for some \(n\text{,}\) while \(I\) and \(J\) have \(3\) and \(2\) elements respectively.
Finally, to emphasize its importance we record here an easy result that we have used repeatedly at this point, and which will be very important later on.
We will often need only a weaker version of this: that every module is a quotient of a projective module.
PrevTopNext