Skip to main content

Postmodern Algebra

Sam Macdonald

Section 3.2 Injective Modules

Subsection Definition and Baer’s Criterion

“”
―
Injective modules are dual to projectives.

Definition 3.14. Injective Module.

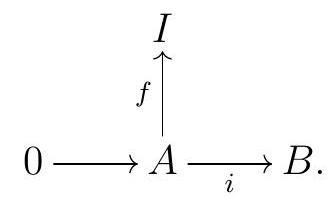
An \(R\)-module \(I\) is injective if given an injective \(R\)-module homomorphism \(i: A \longrightarrow B\) and an \(R\)-module homomorphism \(f: A \longrightarrow I\text{,}\) there exist an \(R\)-module homomorphism \(g\) such that
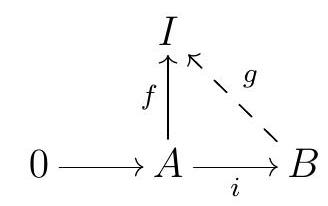
commutes.
These are precisely the modules \(I\) such that \(\operatorname{Hom}_{R}(-, I)\) is exact.

Proof.

By Theorem 2.25, \(\operatorname{Hom}_{R}(-, I)\) is left exact, so for any short exact sequence
\begin{equation*} 0 \longrightarrow A \stackrel{i}{\longrightarrow} B \stackrel{p}{\longrightarrow} C \longrightarrow 0 \end{equation*}
we get an exact sequence
\begin{equation*} 0 \longrightarrow \operatorname{Hom}_{R}(C, I) \stackrel{p^{*}}{\longrightarrow} \operatorname{Hom}_{R}(B, I) \stackrel{i^{*}}{\longrightarrow} \operatorname{Hom}_{R}(A, I) \end{equation*}
So the content of the theorem is that \(I\) is injective if and only if for every injective \(R\)-module homomorphism \(i: A \longrightarrow B\text{,}\) the induced map \(i^{*}\) is surjective. Now notice that \(i^{*}\) is surjective if and only if every \(f \in \operatorname{Hom}_{R}(A, I)\) lifts to some \(g \in \operatorname{Hom}_{R}(B, I)\text{,}\) meaning
commutes. That is precisely what we want for \(I\) to be injective.
Giving examples of injective modules is much harder than giving examples of projective modules, but we will see some examples later. First, we prove some properties of injective modules.
The class of injectives modules is closed for products and finite direct sums.

Proof.

Let \(\pi_{j}: \prod_{i \in I} M_{i} \longrightarrow M_{j}\) be the projection onto the \(j\) th factor. Given any diagram
the fact that \(M_{i}\) is injective gives us \(R\)-module homomorphisms \(g_{i}\) such that
commutes for each \(i\text{.}\) Now the \(R\)-module homomorphism
\begin{equation*} \begin{gathered} B \stackrel{g}{\longrightarrow} \prod_{i \in I} M_{i} \\ b \longmapsto\left(g_{i}(b)\right) \end{gathered} \end{equation*}
makes the diagram
commute, so \(\prod_{i \in I} M_{i}\) is injective.

Proof.

Any diagram
can be extended to a map \(A \longrightarrow E\) by composing \(f\) with the inclusion of the first factor. Since \(E\) is injective, there exists \(h\) such that
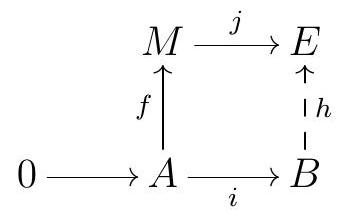
commutes. Let \(\pi: E \longrightarrow M\) be the projection onto \(M\text{,}\) so that \(\pi j=\mathrm{id}_{M}\text{.}\) Now if we set \(g:=\pi h\text{,}\)
\begin{equation*} \begin{aligned} g i & =\pi h i & \text { by definition } \\ & =\pi j f & \text { by commutativity } \\ & =f & \text { because } \pi j=\mathrm{id}_{M} \end{aligned} \end{equation*}

Proof.

On the one hand, if \(E\) is injective then our condition is simply a special case of the definition of injective module. On the other hand, suppose that this condition holds, and consider any diagram
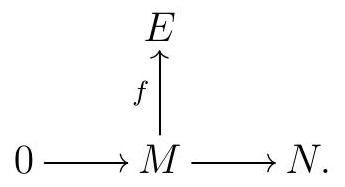
To simplify notation, let’s assume our map \(M \longrightarrow N\) is indeed the inclusion of the submodule \(M\text{,}\) so we can write \(m \in N\) for the image of \(m\) in \(N\text{.}\) Consider the set
\begin{equation*} X:=\{(A, g) \mid A \text { is a submodule of } N, M \subseteq A \subseteq N \text {, and } g \text { extends } f\} \end{equation*}
First, notice \(X\) is nonempty, since \((M, f) \in X\text{.}\) Moreover, we can partially order \(X\) by setting \((A, g) \leqslant(B, h)\) if \(A \subseteq B\) and \(\left.h\right|_{A}=g\text{.}\) So we have a nonempty partially ordered set; let’s show we can apply Zorn’s Lemma to it.
Given a chain in \(X\text{,}\) meaning a sequence
\begin{equation*} \left(A_{1}, g_{1}\right) \leqslant\left(A_{2}, g_{2}\right) \leqslant \cdots \end{equation*}
of nested submodules \(A_{1} \subseteq A_{2} \subseteq \cdots\) and maps \(g_{i}\) that extend all \(g_{j}\) with \(j \leqslant i\text{,}\) let \(A:=\bigcup_{i} A_{i}\text{,}\) and define
\begin{equation*} \begin{aligned} & A \longrightarrow g \\ & a \longrightarrow g_{i}(a) \text { if } a \in A_{i} . \end{aligned} \end{equation*}
Since all the \(g_{i}\) are homomorphisms of \(R\)-modules, this map \(g\) is indeed a map of \(R\)-modules. Moreover, \(g\) is well-defined, since the \(g_{i}(a)=g_{j}(a)\) whenever \(a \in A_{i} \cap A_{j}\text{.}\) By construction, this map extends all the \(g_{i}\text{,}\) so we conclude that \((A, g)\) is an upper bound for our chain. Moreover, \(M \subseteq A \subseteq N\) follows immediately from our construction, and since each \(g_{i}\) extends \(f\text{,}\) so does \(g\text{.}\) We conclude that \((A, g) \in X\text{,}\) and more generally that any chain in \(X\) has an upper bound in \(X\text{.}\) So Zorn’s Lemma applies.
By Zorn’s Lemma, \(X\) has a maximal element, say \((A, g)\text{.}\) We claim that \(A=N\text{.}\) Suppose not, and let \(n \in N\) be an element not in \(A\text{.}\) One can check that
\begin{equation*} I:=\{r \in R \mid r n \in A\} \end{equation*}
is an ideal in \(R\text{,}\) and that
\begin{equation*} \begin{aligned} & I \stackrel{h}{\longrightarrow} E \\ & r \longrightarrow g(r n) \end{aligned} \end{equation*}
is an \(R\)-module homomorphism.
By assumption, we can extend \(h\) to an \(R\)-module homomorphism \(R \longrightarrow E\text{,}\) which we will write as \(h\) as well. Now the \(R\)-module homomorphism
\begin{equation*} \begin{aligned} & A+R n \longrightarrow E \\ & a+r n \longrightarrow g(a)+h(r) \end{aligned} \end{equation*}
is well-defined by construction, since any \(r n \in A\) satisfies \(g(r n)=h(r)\text{,}\) and if \(r n=r^{\prime} n\) then \(h(r)=r n=r^{\prime} n=h\left(r^{\prime}\right)\text{.}\) Finally, this map agrees with \(g\) on \(A\text{,}\) and thus it agrees with \(f\) on \(M\text{,}\) so \((A+R n, \varphi) \in X\) and \((A, g) \leqslant(A+R n, \varphi)\text{.}\) By the maximality of \((A, g)\text{,}\) we conclude that \(A+R n=A\text{,}\) and thus \(n \in A\text{,}\) which is a contradiction. We conclude that \(A=N\text{.}\) Therefore, \(g\) makes the diagram
commute.

Subsection Divisible Modules

“”
―
It is very easy to see that every \(R\)-module is a quotient of a free module. The dual statement is true as well, but it is a little more delicate.

Definition 3.19. Divisible Module.

An \(R\)-module \(D\) is divisible if for every nonzero \(r \in R\) and every \(d \in D\) there exists \(b \in D\) such that \(r b=d\text{.}\)

Remark 3.20.

Remark 4.22. Given \(r \in R\text{,}\) and an \(R\)-module \(M\text{,}\) the multiplication by \(r\) map \(M \stackrel{\cdot r}{\longrightarrow} M\) is an \(R\)-module homomorphism. The module \(M\) is divisible if and only if multiplication by \(r\) is surjective for all nonzero \(r \in R\text{.}\)

Example 3.21. Divisible Modules.

The set of rational numbers \(\Q\text{,}\) considered as a module over the ring of integers \(\Z\text{,}\) is a divisible module. This is because for any nonzero integer \(n\text{,}\) you can find a rational number \(q = \frac 1n\) such that \(nq\) is still a rational number.

Proof.

Let \(D\) be a divisible \(R\)-module and \(E\) be a submodule of \(D\text{.}\) Let \(r \in R\) and \(d+E \in\) \(D / E\text{.}\) By assumption, there exists \(a \in D\) such that \(r a=d\text{.}\) The image \(a+E\) of \(a\) in \(D / E\) is still a solution to \(r(a+E)=d+D\text{,}\) so indeed \(E\) is divisible.

Proof.

Suppose that \(E\) is an injective \(R\)-module, where \(R\) is a domain. Fix \(r \in R\) and \(a \in E\text{.}\) Since \(R\) is a domain, we have \(s r=s^{\prime} r \Rightarrow s=s^{\prime}\) for any \(s, s^{\prime}, r \in R\text{.}\) In particular, each element in \((r)\) can be written uniquely as \(s r\) for some \(s \in R\text{.}\) In particular, the map of \(R\)-modules
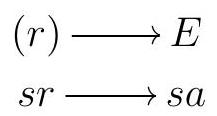
is well-defined. Since \(E\) is injective, we can extend this to a homomorphism \(f: R \longrightarrow E\text{.}\) Finally, \(f(1) \in E\) is an element such that \(e=f(r)=r f(1)\text{,}\) and \(E\) is divisible.
This not true in general if we do not assume \(R\) is a domain.

Example 3.25. Injective but not Divisible Module.

Example 4.25. Let \(k\) be a field and \(R=k[x] /\left(x^{2}\right)\text{.}\) On the one hand, \(R\) is not a divisible \(R\)-module, since there is no \(y \in R\) such that \(x y=1\text{.}\) On the other hand, \(R\) is actually an injective module over itself, although we do not have the tools to justify that this is indeed an injective \(R\)-module. \({ }^{1}\)
The converse of Lemma 3.24 does not hold in general, and quotients of injective modules are not necessarily injective.

Exercise 3.26. Injective Modules not Closed Under Quotients.

Let \(R=k[x, y]\text{,}\) where \(k\) is a field, let \(Q=\operatorname{frac}(R)\) be the fraction field of \(R\text{.}\) The \(R\)-module \(M=Q / R\) is divisible but not injective.
But the converse of Lemma 3.24 does hold for some special classes of rings.

Proof.

Given Lemma 3.24, we only need to show that divisible modules are injective. By Baer’s Criterion, we only need to show that any map from an ideal to \(E\) can be extended to the whole ring. So let \(E\) be a divisible \(R\)-module, and consider any map \(I \longrightarrow E\) from an ideal \(I\) to \(E\text{.}\) If \(I=0\text{,}\) we could extend our map by taking the \(0\) map from \(R\) to \(E\text{,}\) so we might as well assume that \(I \neq 0\text{.}\) By assumption, \(I=(a)\) for some \(a \in R\text{,}\) and since \(E\) is divisible, there exists \(e \in E\) such that \(f(a)=a e\text{.}\) Now consider the multiplication by \(r\) map,
\begin{equation*} \begin{aligned} & R \longrightarrow g \\ & r \longrightarrow r e . \end{aligned} \end{equation*}
For every \(r \in R, g(r a)=r a e=r f(a)=f(r a)\text{,}\) so \(g\) extends \(f\text{.}\) Therefore, by Theorem 4.18, \(E\) is injective.

Proof.

If \(E\) is injective, it is also divisible, by Lemma 3.24. Given any submodule \(D \subseteq E\text{,}\) any \(e \in E\text{,}\) and a nonzero \(r \in R\text{,}\) there exists \(y \in E\) such that \(r y=e\text{,}\) and so this also holds in \(E / D\text{.}\) Then \(E / D\) is divisible, and thus injective by Theorem 3.27.
 1 
Using fancy words you might learn in Commutative Algebra II, this ring \(R\) is an example of a complete intersection, which is a subclass of Gorenstein rings. Moreover, \(\operatorname{dim} R=0\) - this is something you’d learn about in Commutative Algebra II. Now it turns out (and this is a nontrivial fact) that Gorenstein rings of dimension 0 are injective modules over themselves.
Given an injective abelian group, we can always use it to construct an injective \(R\)-module over our favorite ring \(R\text{.}\)

Proof.

Let \(E:=\operatorname{Hom}_{\mathbb{Z}}(R, D)\text{.}\) This abelian group \(E\) is an \(R\)-module, via
\begin{equation*} r \cdot f:=(a \mapsto f(r a)) \end{equation*}
We claim that \(E\) is actually an injective \(R\)-module. By Theorem 3.15, it is sufficient to prove that \(\operatorname{Hom}_{R}\left(-, \operatorname{Hom}_{\mathbb{Z}}(R, D)\right)\) is an exact functor. By Corollary 2.82, \(\operatorname{Hom}_{R}\left(-, \operatorname{Hom}_{\mathbb{Z}}(R, D)\right)\) is naturally isomorphic to \(\operatorname{Hom}_{\mathbb{Z}}\left(-\otimes_{\mathbb{Z}} R, D\right)\text{.}\) This last functor is the composition of
\begin{equation*} \operatorname{Hom}_{\mathbb{Z}}\left(-\otimes_{\mathbb{Z}} R, D\right)=\operatorname{Hom}_{\mathbb{Z}}(-, D) \circ\left(-\otimes_{\mathbb{Z}} R\right) \end{equation*}
On the one hand, \(-\otimes_{\mathbb{Z}} R\) is naturally isomorphic to the identity on \(R\)-Mod, by Lemma 2.54, so it is exact. On the other hand, \(D\) is an injective \(\mathbb{Z}\)-module, so \(\operatorname{Hom}_{\mathbb{Z}}(-, D)\) is exact by Theorem 3.15. The composition of exact functors is exact, and thus \(\operatorname{Hom}_{R}\left(-, \operatorname{Hom}_{\mathbb{Z}}(R, D)\right)\) is exact.

Example 3.30.

Example 4.29. Since \(\mathbb{Q}\) is a divisible abelian group, by Lemma 3.29 for any ring \(R\) the \(R\)-module \(\operatorname{Hom}_{\mathbb{Z}}(R, \mathbb{Q})\) is injective.

Subsection Every Module Embeds into an Injective Module

“”
―
When we talked about projective modules, we showed that every module is a quotient of a projective - in fact, every module is a quotient of a free module. The dual statement is true as well: that every module embeds into an injective module. We will soon see that these two statements are extremely important.
While the statement about projectives is relatively simple - it’s essentially a consequence of the universal property of free modules - the fact about injectives is a lot more delicate; the work we just did on divisible modules was precisely so we could show this deep and important fact.
First, we show that every abelian group can be embedded into an injective abelian group.

Proof.

On the one hand, \(M\) is a quotient of some free abelian group, say \(M \cong\left(\oplus_{i} \mathbb{Z}\right) / K\text{.}\) Now \(\mathbb{Z}\) embeds in \(\mathbb{Q}\text{,}\) and thus \(M\) embeds into a quotient of \(\oplus_{i} \mathbb{Q}\text{.}\) By Example 4.20, \(\mathbb{Q}\) is an injective abelian group, and by Corollary \(4.19, \oplus_{i} \mathbb{Q}\) is an injective abelian group, since \(\mathbb{Z}\) is a noetherian ring. By Corollary 3.28, any quotient of \(\oplus_{i} \mathbb{Q}\) is also injective, so we have shown that \(M\) embeds into an injective abelian group, say \(D\text{.}\)
In fact, the proof above can be repeated over any PID: if \(R\) is a PID, we can show that any \(R\)-module \(M\) embeds into an injective module, and in fact \(M\) embeds into some number of copies of the fraction field \(Q\text{.}\)
We can finally show that over any ring, every module can be embedded into an injective module.

Proof.

First, by Lemma 3.31 we can view \(M\) as a subgroup of some injective abelian group \(D\text{.}\) Let \(i: M \longrightarrow D\) be the inclusion map and \(E:=\operatorname{Hom}_{\mathbb{Z}}(R, D)\text{.}\)
By Lemma 3.29, \(E\) is an injective \(R\)-module. Since Hom is left exact, by Theorem 2.25, \(\operatorname{Hom}_{\mathbb{Z}}(R,-)\) preserves the inclusion \(I\text{,}\) so we have an inclusion \(\operatorname{Hom}_{\mathbb{Z}}(R, M) \subseteq \operatorname{Hom}_{\mathbb{Z}}(R, D)\text{.}\) Now consider the map
\begin{equation*} \begin{aligned} & M \stackrel{\psi}{\longrightarrow} \operatorname{Hom}_{\mathbb{Z}}(R, M) \\ & m \longrightarrow(r \mapsto r m) . \end{aligned} \end{equation*}
This is an \(R\)-module homomorphism:
  • Given \(a, b \in M\text{,}\)
    \begin{equation*} \psi(a+b)(r)=r(a+b)=r a+r b=\psi(a)(r)+\psi(b)(r) \end{equation*}
    so \(\psi(a+b)=\psi(a)+\psi(b)\text{.}\)
  • Given \(r \in R, m \in M\text{,}\) and \(s \in R\text{,}\)
    \begin{equation*} \psi(r m)(s)=s(r m)=r(s m)=r \psi(m)(s), \end{equation*}
    so \(\psi(r m)=r \psi(m)\text{.}\)
Moreover, if \(\psi(m)=0\) then \(m=\psi(m)(1)=0\text{.}\) So \(\psi\) is injective, and thus composing \(\psi\) with our previous inclusion \(\operatorname{Hom}_{\mathbb{Z}}(R, M) \subseteq \operatorname{Hom}_{\mathbb{Z}}(R, D)\) gives us an inclusion \(\varphi\) of \(M\) into the injective \(R\)-module \(\operatorname{Hom}_{\mathbb{Z}}(R, D)\text{.}\) However, the inclusion \(\operatorname{Hom}_{\mathbb{Z}}(R, M) \subseteq \operatorname{Hom}_{\mathbb{Z}}(R, D)\) is a priori only a map of abelian groups, so we should check that \(\varphi\) is indeed \(R\)-linear. In order to do this, we need to be careful (at least in the case when \(R\) is not commutative) with how we defined the left \(R\)-module structure on \(\operatorname{Hom}_{\mathbb{Z}}(R, D)\) in Exercise 56: this is a situation where we view \(R\) as a \((\mathbb{Z}, R)\)-bimodule and \(D\) as a left \(\mathbb{Z}\)-module, so \(\operatorname{Hom}_{\mathbb{Z}}(R, D)\) is a left \(R\)-module via
\begin{equation*} r \cdot f \text { is the } R \text {-map given by }(r \cdot f)(a)=f(a r) \text {. } \end{equation*}
The map we need to show is \(R\)-linear is
\begin{equation*} \begin{aligned} & M \stackrel{\varphi}{\longrightarrow} \operatorname{Hom}_{\mathbb{Z}}(R, D) \\ & m \longmapsto \varphi_{m}=(r \mapsto i(r m)) . \end{aligned} \end{equation*}
Regarding \(i\) as a simple inclusion, \(i(m)\) simply views the element \(m\) as an element of \(D\text{;}\) to simplify notation, we drop the \(i\) : so for each \(m \in M, \varphi(m)\) is the map \(\varphi_{m}: R \longrightarrow D\) given by
\begin{equation*} \varphi_{m}(r)=r m \end{equation*}
For every \(r \in R, m \in M\text{,}\) and \(s \in R\text{,}\)
\begin{equation*} \begin{array}{rrr} \varphi_{r m}(s) & =s(r m) & \text { by definition } \\ & =(s r) m & \\ & =\varphi_{m}(s r) & \text { using the module axioms } \\ & =r \varphi_{m}(s) & \text { by definition } \\ & & \text { by defition of the left } R \text {-module structure on } \operatorname{Hom}_{\mathbb{Z}}(R, D) \end{array} \end{equation*}
so \(\varphi(r m)=r \varphi(m)\text{.}\) This shows that \(\varphi\) is an inclusion of \(R\)-modules.
And finally, just like we did for projectives, we can characterize injectives in terms of split short exact sequences.

Proof.

Let \(I\) be an injective \(R\)-module, and consider any short exact sequence
\begin{equation*} 0 \longrightarrow I \stackrel{i}{\longrightarrow} B \stackrel{p}{\longrightarrow} C \longrightarrow 0 \end{equation*}
Since \(I\) is injective, there exists a map \(g\) making
commute, and such a \(g\) gives a splitting for our short exact sequence.
Conversely, suppose that every short exact sequence \(0 \longrightarrow I \longrightarrow B \longrightarrow C \longrightarrow 0\) splits, and consider a diagram
By Theorem 3.32, \(I\) embeds into some injective \(R\)-module \(E\text{,}\) say by the inclusion \(j\text{.}\) By assumption, the short exact sequence
\begin{equation*} 0 \longrightarrow I \stackrel{j}{\longrightarrow} E \longrightarrow \text { coker } j \longrightarrow 0 \end{equation*}
splits, so there exists a map \(q: E \longrightarrow I\) such that \(q i=\mathrm{id}_{I}\text{.}\) Since \(E\) is injective, we can lift \(i\) through \(j f\text{,}\) obtaining an \(R\)-module homomorphism \(\ell\) such that
commutes. Now \(g:=q \ell\) satisfies
\begin{equation*} \begin{array}{rlr} g i & =q \ell i & \text { by definition } \\ & =q j f & \text { by commutativity } \\ & =f & \text { since } q j=\mathrm{id}_{I}, \end{array} \end{equation*}
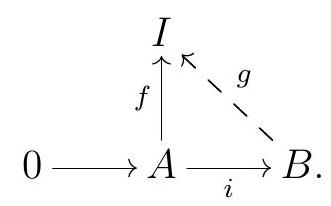
commutes.
Before we move on from injective modules, let us say a word about how the story continues. The next chapter is quite beautiful, and it is a shame we have no time to discuss it in detail this semester.
We proved above that every module \(M\) is a submodule of some injective module. One can even do better and talk about the smallest injective module that \(M\) embeds in; this is called the injective hull \(E(M)\) of \(M\text{.}\) One could describe \(E(M)\) by saying that it is the intersection of all the injective modules that contain \(M\text{,}\) but this is not a very practical description. Injective hulls can also be described through the theory of essential extensions, a topic which we do not have time to discuss this semester. We leave the definition here just for fun, but we do not have the time to talk about it at length.

Definition 3.34.

Let \(M \subseteq E\text{.}\) We say \(E\) is an essential extension of \(M\) if every nonzero submodule \(N \subseteq E\) intersects \(M\) nontrivially, meaning \(E \cap M \neq 0\text{.}\) More generally, an injective map \(\alpha: M \longrightarrow E\) is an essential extension if \(\alpha(M) \subseteq E\) is an essential extension in the sense above.
One then shows that an \(R\)-module \(M\) is injective if and only if it has no proper essential extensions \(E \supseteq M\text{.}\) This proves that a maximal essential extension \(E\) of \(M\) is injective, and that there are no other injective modules \(I\) with of \(M \subseteq I \subseteq E\text{.}\) Moreover, one can show that any two maximal essential extension of \(M\) are isomorphic - and thus we can talk about the maximal essential extension of \(M\text{,}\) up to isomorphism, which is
But the theory of injectives, and injective hulls in particular, is much more complicated than the theory of projectives. When \(M\) is a finitely generated module, we can always find a finitely generated projective (even free!) module surjecting onto \(M\text{;}\) in contrast, the injective hull \(E(M)\) might not be finitely generated - in fact, \(E(M)\) is typically not finitely generated even when \(M\) is cyclic.
The story of the structure of injective modules then continues in a beautiful way. Over a noetherian ring, it turns out that every injective module can be decomposed into a direct sum of injective modules of the form \(E(R / P)\text{,}\) where \(P\) is a prime ideal in \(R\text{.}\) Moreover, the injective modules \(E(R / P)\) are the indecomposable injective modules, so the basic building blocks of injective modules. One can in fact compute the injective hull of any finitely generated \(R\)-module very explicitly. A lot of this was proved in Eben Matlis’ beautiful PhD thesis [Mat58], but sadly we do not have time for the details this semester. The details, however, are very important, for example to develop the theory of local cohomology - a topic which we will briefly mention later on.
PrevTopNext