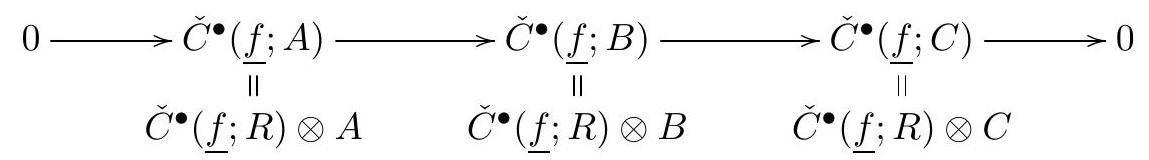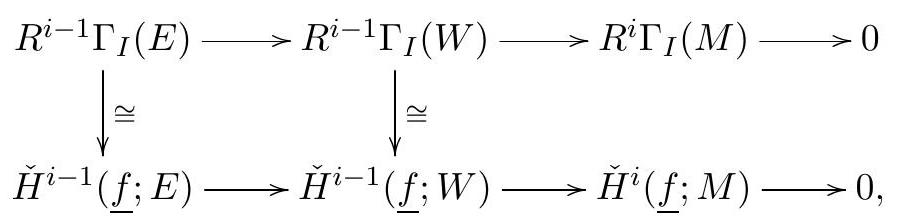We have seen that \(\Gamma_{I}(M) \cong \underset{n}{\lim _{n}} \operatorname{Ext}_{R}^{i}\left(R / I^{n}, M\right)\) and \(\check{H}^{i}(\underline{f} ; M) \cong \underset{n}{\lim _{n}} \mathrm{H}^{i}\left(f_{1}^{n}, \ldots, f_{t}^{n} ; M\right)\text{.}\) To show that \(R^{i} \Gamma_{I}(M) \cong \check{H}^{i}(f ; M)\text{,}\) we proceed in the following steps:
Step 1: Show \(\Gamma_{I}(M)\) and \(\check{H}^{0}(\underline{f} ; M)\) are canonically isomorphic.
Step 2: Show that \(\check{H}^{>0}(\underline{f} ; E)=0\) for any injective module \(E\text{.}\)
Step 3: Use the previous steps to conclude the proof.
Proof of Step 1:
\begin{equation*}
\begin{aligned}
\check{H}^{0}(\underline{f} ; M) & =\mathrm{H}^{0}\left(0 \rightarrow M \rightarrow \oplus_{i} M_{f_{i}}\right) \\
& =\left\{m \in M \mid\left[\frac{m}{1}\right]=0 \text { in } M_{f_{i}} \text { for all } i\right\} \\
& =\left\{m \in M \mid f_{i}^{\gg 0} \cdot m=0 \text { for all } i\right\} \\
& =\Gamma_{I}(M) .
\end{aligned}
\end{equation*}
We note that the last equality uses finite generation of \(I\) in a crucial way; only the containment " \(\supseteq\) " holds in general without this.
Proof of Step 2: By the structure theorem for injectives over noetherian rings, \(E \cong \oplus E_{\lambda}\text{,}\) where
\begin{equation*}
E_{\lambda}=E_{R}(R / P) \cong E_{R_{P}}\left(R_{P} / P R_{P}\right)
\end{equation*}
By the direct sum property, we may replace \(E\) by \(E_{R}(R / P)\text{.}\) By the invariance of base property, we may replace \(R\) by \(R_{P}\text{.}\) Now, \(E\) is an injective hull of the residue field, so it is artinian, and we write \(E=\lim _{\longrightarrow} E_{t}\) where the \(E_{t}\) are modules of finite length. It suffices to show that the vanishing holds for modules of finite length.
We claim that if the desired vanishing holds for \(M=K\text{,}\) then it holds for all modules of finite length (which would complete Step 2). We induce on the length of \(L\text{.}\) If \(1<\ell(M)<\infty\text{,}\) then write \(0 \rightarrow L \rightarrow M \rightarrow K \rightarrow 0\text{,}\) with \(\ell(L)<\ell(M)\text{.}\) The long exact sequence gives
\begin{equation*}
\cdots \rightarrow \check{H}^{i}(\underline{f} ; L) \rightarrow \check{H}^{i}(\underline{f} ; M) \rightarrow \check{H}^{i}(\underline{f} ; K) \rightarrow \cdots,
\end{equation*}
and by the induction hypothesis,
\begin{equation*}
\cdots \rightarrow 0 \rightarrow \check{H}^{i}(\underline{f} ; M) \rightarrow 0 \rightarrow \cdots,
\end{equation*}
for \(i>0\text{,}\) establishing the claim.
Applying the invariance of base property again, we may assume without loss of generality that \(R=K\text{.}\)
There are multiple ways to deal with this case. We note that if \(f_{i}=0\text{,}\) then \(\check{C}^{\bullet}\left(f_{i} ; K\right)=(0 \rightarrow K \rightarrow 0)\text{,}\) and if \(f_{i} \neq 0\text{,}\) then \(\check{C}^{\bullet}\left(f_{i} ; K\right)=(0 \rightarrow K \stackrel{1}{\longrightarrow} K \rightarrow 0)\text{.}\) It is then an easy exercise, which we leave to you, to show that \(\check{H}^{i}(f ; K)=K\) for \(i=0\) and 0 for \(i>0\) if all \(f_{i}\) ’s are zero, and that \(\check{H}^{i}(\underline{f} ; K)=0\) for all \(i\) otherwise.
Of course, this step relied crucially on the structure theorem for injectives over noetherian rings.
Proof of Step 3: This follows in complete generality from the previous steps.
We proceed by induction on \(i\text{,}\) with the base case being Step 1 . Now, let \(i>0\text{.}\)
We assume that we have a canonical isomorphism between \(H_{I}^{j}(M)\) and \(\check{H}^{j}(\underline{f} ; M)\) for all \(M\) and all \(j<i\text{.}\) Embed \(M\) into an injective \(E\) to get a short exact sequence
\begin{equation*}
0 \rightarrow M \rightarrow E \rightarrow W \rightarrow 0
\end{equation*}
Then, there is a commutative diagram
where bottom zero on the right comes from Step 2. This induces an isomorphism \(H_{I}^{i}(M) \cong \check{H}^{i}(f ; M)\text{.}\) We omit the verification that this isomorphism does not depend on the choice of embedding into an injective, and that these isomorphisms are compatible with the connecting maps of long exact sequences.


.jpg)